Lean for Scala programmers - Part 3

In the previous installment we discussed inductive types and pattern matching.

Today we're going to talk about Dependent Types and Type Classes.

Scala version used: 3.9.0
Lean 4 version: 4.31.0
Latest revision: Sep 23, 2026

1. Dependent functions

1.1 Idea

A function $f: A \to B$ between two sets $A, B$ is commonly defined in mathematics as a collection of pairs $f := \{(a, b)\} \subset A \times B$ with the property that elements $a$ of $A$ appear exactly once.

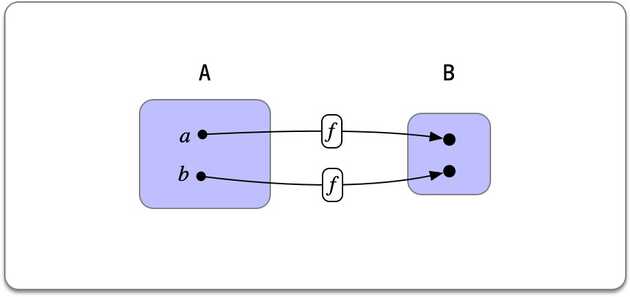
A dependently typed function is a generalization of this concept:

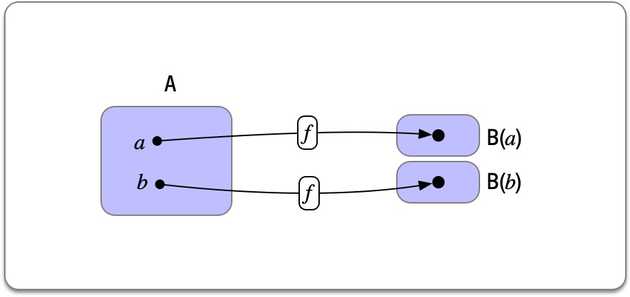
Each element $f(a)$ is allowed to be a member of a different set that depends on $a$.

This construction gives rise to a set-level function $B$ that assigns a set $B(a)$ to each element $a \in A$.

Observe that if this function $B$ is constant (i.e. it maps all elements $a$ to a single set) then we are back to the regular definition of non-dependent functions.

Example: Vector fields

At every point $p$ of a circle $S^1$, consider a vector $V(p)$ on the tangent space $T_{p}S^{1}$ at this point:

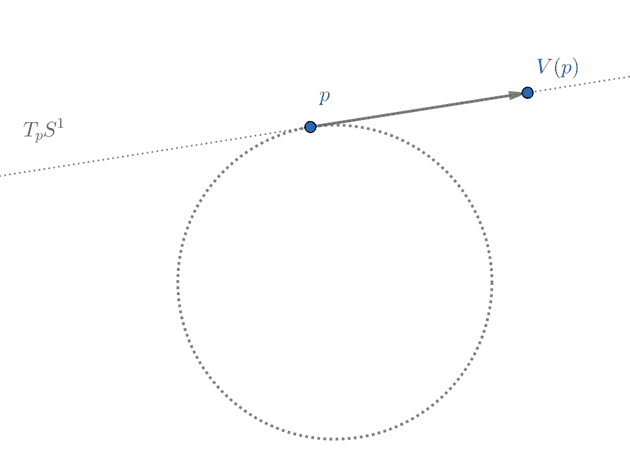
Since each $V(p)$ lives in a different tangent space $T_{p}S^{1}$ (that depends on $p$), it makes sense to regard $V$ as a dependent function.

Example: operations on tuples

A very common example of dependent types in Scala 3 is obtaining components of tuples at specific positions:

val t: (Int, String, Boolean) = (0, "", false)

assert( t.apply(0) == 0 )
assert( t.apply(1) == "" )
assert( t.apply(2) == false )

We can see how apply produces a value of a type that depends on the input index:

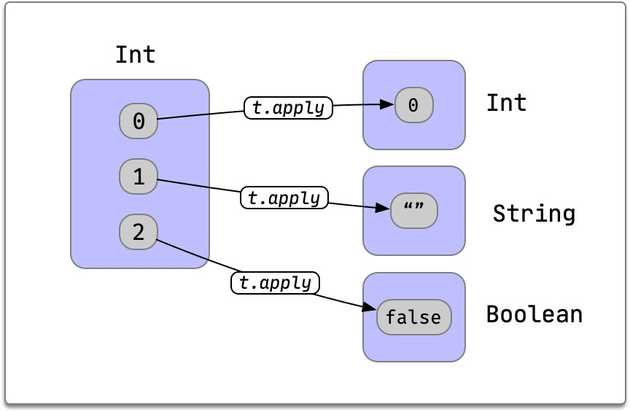
In fact most generic tuple operations use dependent types.

1.2 Dependent functions in Lean

In Lean the type of a regular function $f$ from $A$ to $B$ is written as

f: A -> B

here the codomain B is the same for every element a of the domain A.

In a dependent function we need a way to indicate exactly how the codomain depends on each element of the domain.

The signature of a dependent function $f$ from $A$ to $B(a)$ is written in Lean like this:

f: (a: A) -> B a

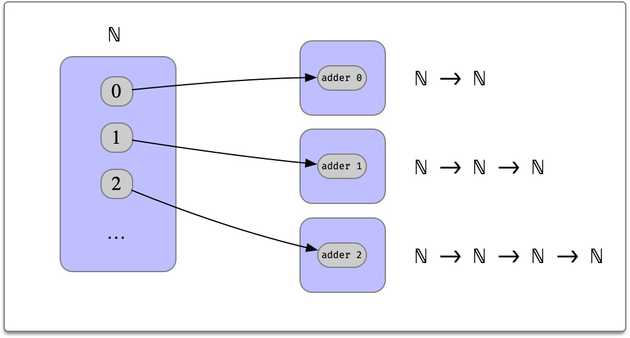
We already met one in Part 1: map_length, whose result type mentions the list that we pass in.

Example: variable number of arguments

Consider a function adder that takes:

1. A number $n$ representing extra arguments
2. An initial value $acc$
3. $n$ arguments

and returns the sum of the initial value and extra arguments.

adder 2 acc 4 3 = acc + 4 + 3

For example

adder 0 5        = 5
adder 1 10 11    = 21
adder 2 18 17 12 = 47

i.e. the first argument is the number of extra arguments after the 2nd argument.

(This example is described in Edwin Brady's Type-Driven Development with Idris)

We will proceed in two steps:

1. Define a type level function that calculates the return type: a function with $n$ parameters:

def Adder: Nat -> Type
  | 0     => Nat
  | k + 1 => Nat -> Adder k


example: Adder 0 =  Nat                := rfl
example: Adder 1 = (Nat -> Nat)        := rfl
example: Adder 2 = (Nat -> Nat -> Nat) := rfl

2. Define a regular function, whose signature is computed by Adder based on the 1st argument:

def adder: (n: Nat) -> (acc: Nat) -> (Adder n)
  | 0,     acc => acc
  | k + 1, acc => fun x => adder k (x + acc)

-- some examples of types:

-- adder 0 : Nat -> Nat
-- adder 1 : Nat -> Nat -> Nat
-- adder 2 : Nat -> Nat -> Nat -> Nat

example: (adder 0) 5        = (5 : Nat) := rfl
example: (adder 1) 10 11    = (21: Nat) := rfl
example: (adder 2) 18 17 12 = (47: Nat) := rfl

So adder n produces a function whose type depends on n:

1.3 Dependent Functions in Scala 3

Dependent function types

Scala 3 has dependent function types too:

trait Entry:
  type Key
  val key: Key

val extractKey: (e: Entry) => e.Key = e => e.key

(e: Entry) => e.Key is the direct analog of Lean's (a: A) -> B a: the result type depends on the argument e. But the dependency can only go through the type members of the argument, like e.Key. A function like adder, whose result type depends on an Int value, needs another tool: match types.

Match types

Scala 3 supports a similar form of dependent typing using match types.

We follow the same steps as in Lean:

1. Define a type level function that calculates the return type:

import compiletime.ops.int.S

type Adder[N <: Int] = N match
  case 0    =>  Int
  case S[k] => (Int => Adder[k & Singleton])


summon[ Adder[0] =:=  Int               ]
summon[ Adder[1] =:= (Int => Int)       ]
summon[ Adder[2] =:= (Int => Int => Int)]

2. Define a function, whose signature is computed by Adder based on the 1st argument:

import compiletime.constValue

inline def adder[N <: Int & Singleton](n: N)(acc: Int): Adder[N] =
  inline n match
    case _: 0    => acc
    case _: S[k] => x => adder(constValue[k & Singleton])(x + acc)


assert( adder(0)(5)          == 5  )
assert( adder(1)(10)(11)     == 21 )
assert( adder(2)(18)(17)(12) == 47 )

Here we can see how the fact that types are not first class in Scala introduces some complexities:

• Singleton is needed so that adder(0) is inferred as adder[0](0) and not adder[Int](0).
• After pattern matching on the type _: S[k] we obtain the type k of the predecessor n - 1.
• In order to continue the process we need to obtain the value associated with the singleton type k. For this we use constValue.
• But constValue only works for values known at compile time, so we have to use inline match and also inline the whole function.

2. Type Classes

Type classes give us a second way to compute a type from a value: instead of writing a function like Adder, we let instance resolution build the type step by step.

2.1 Type Classes in Lean

Lean has support for type classes by using the keywords class / instance.

Let's implement the adder function using implicit type class resolution this time:

class Bundle (n: Nat) where
  Adder: Type
  adder: Nat -> Adder

This declaration defines a few things:

Note how both Bundle.Adder and Bundle.adder acquired two extra parameters:

• The class argument n. It is explicit in Bundle.Adder, because nothing else in its type mentions n. In Bundle.adder it is implicit, because n appears in the result type Bundle.Adder n.
• An instance argument [self : Bundle n] (indicated by the square brackets), which Lean finds by type class resolution.

We need two Bundle instances, corresponding to the base case and the inductive step:

instance : Bundle 0 where
  Adder := Nat
  adder := id

instance (k: Nat) [predecessor: Bundle k] : Bundle (k + 1) where
  Adder := Nat -> predecessor.Adder
  adder := fun acc x => Bundle.adder (x + acc)

Notes:

• id is the identity function
• Bundle.adder (x + acc) is using the instance in scope (predecessor), so we don't need to pass it manually.

In order to use the function Bundle.adder the number n needs to be known, either by inference or explicitly providing it like so:

#eval Bundle.adder (n := 0) 5
-- 5
#eval Bundle.adder (n := 1) 10 11
-- 21

(n := 0) is a named argument, like in Scala: it sets the implicit argument n of Bundle.adder.

Alternatively we can create a helper function where n is required explicitly:

def adderTC (n acc: Nat) [c: Bundle n]: Bundle.Adder n :=
  @Bundle.adder n c acc

#eval adderTC 0 5
-- 5
#eval adderTC 1 10 11
-- 21

@Bundle.adder makes all implicit arguments explicit, so we can pass n and the instance c by position. (We call the helper adderTC because adder already exists from section 1.2.)

Sanity check:

example: (adderTC 0) 5        = (5 : Nat) := rfl
example: (adderTC 1) 10 11    = (21: Nat) := rfl
example: (adderTC 2) 18 17 12 = (47: Nat) := rfl

2.2 Type Classes in Scala

The same type class in Scala:

trait Bundle[N <: Int]:
  type Adder
  def adder: Int => Adder

Due to an idiosyncrasy of Scala we need to create a helper type function BundleWithAdder to manually propagate type information (this is the Aux pattern common in shapeless). Without it, the type of each given would be just Bundle[N], and the compiler would forget what Adder is.

import compiletime.ops.int.S

type BundleWithAdder[N <: Int, A] =
  Bundle[N] { type Adder = A }

// base case: Bundle[0]

given BundleWithAdder[0, Int] =
  new Bundle[0]:
    type Adder = Int
    def adder = identity

// inductive step: Bundle[K] implies Bundle[S[K]]

given [K <: Int](using predecessor: Bundle[K]):
  BundleWithAdder[S[K], Int => predecessor.Adder] =
  new Bundle[S[K]]:
    type Adder = Int => predecessor.Adder
    def adder = acc => x => predecessor.adder(x + acc)

Sanity check:

val bundle0 = summon[Bundle[0]]
val bundle1 = summon[Bundle[1]]
val bundle2 = summon[Bundle[2]]

summon[ bundle0.Adder =:=  Int                ]
summon[ bundle1.Adder =:= (Int => Int)        ]
summon[ bundle2.Adder =:= (Int => Int => Int) ]

Taking the singleton type n.type of the term n will kickstart the process:

def adderTC(n: Int)(acc: Int)(using bundle: Bundle[n.type]) =
  bundle.adder(acc)

assert( adderTC(0)(5)          == 5  )
assert( adderTC(1)(10)(11)     == 21 )
assert( adderTC(2)(18)(17)(12) == 47 )

3. Propositions depending on values

Propositions can be used as goals in themselves (example 3.1) or as a way to create specifications (example 3.2).

3.1 Properties of natural numbers

Consider the statement:

For all natural numbers, $n + 0 = n$

The expression $n + 0 = n$ is a proposition that depends on $n$: the function fun n => n + 0 = n maps each natural number to a proposition. A proof of the statement is then a dependent function $f$ that maps each $n$ to a proof of $n + 0 = n$. Its type is ∀ (n: Nat), n + 0 = n, which (as we saw in Part 1) is the same as (n: Nat) -> n + 0 = n:

example: ∀ (n: Nat), n + 0 = n :=
  fun n => (rfl : n + 0 = n)

Each proof is just rfl, because Nat.add is defined by recursion on its second argument: n + 0 reduces to n by definition. The mirror statement 0 + n = n is also true, but rfl can't prove it, because 0 + n can't reduce while n is unknown. It needs induction, like add 0 m = m in Part 2; we'll prove it in Part 4.

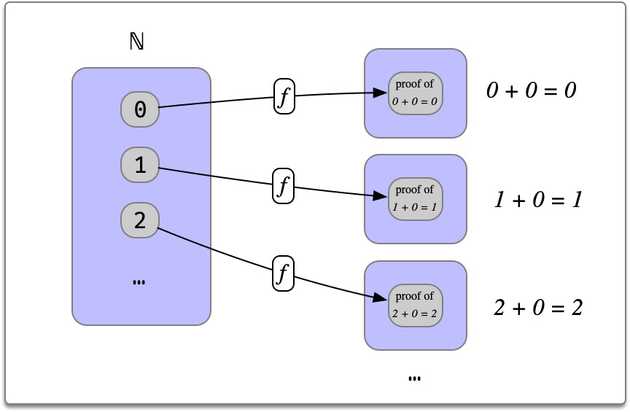
3.2 Algebraic structures

Here's how one could define a monoid in Lean

class Monoid (M: Type) where
  mul : M -> M -> M
  one : M
  mul_assoc : ∀ (a b c : M), mul (mul a b) c = mul a (mul b c)
  one_mul   : ∀ (a : M), mul one a = a
  mul_one   : ∀ (a : M), mul a one = a

In situations like this we rely heavily on dependent types to encode all the laws associated with the structure at hand. Each law is a ∀-statement: for example, a proof of one_mul is a dependent function that takes any a : M and returns a proof of mul one a = a.

Here's a monoid instance for addition of natural numbers:

instance : Monoid Nat where
  mul := (· + ·)
  one := 0
  mul_assoc := Nat.add_assoc
  one_mul   := Nat.zero_add
  mul_one   := Nat.add_zero

Luckily in this case the basic properties have already been proved in Lean's core library, so we can just delegate to them.

• The expression (· + ·) is the short form of the anonymous function fun a b => a + b, similar to Scala's _ + _. (You type · as \..)

Compare this with a Scala type class, for example the Monoid of the cats library:

trait Monoid[M]:
  def combine(a: M, b: M): M
  def empty: M

The laws are not part of the type. Scala libraries check them with property-based tests (cats uses its cats-laws module, built on discipline), which try many random values. In Lean, the laws are fields of the class: an instance that doesn't supply the three proofs doesn't compile.

4. Dependent pairs

There is another important example of dependent types called dependent pairs, or $\Sigma$-types (also dependent sums). Some authors call them dependent products, but that name more often means the Π-types of section 1 (dependent functions), so we won't use it.

Consider the regular cartesian product of two sets $A$, $B$:

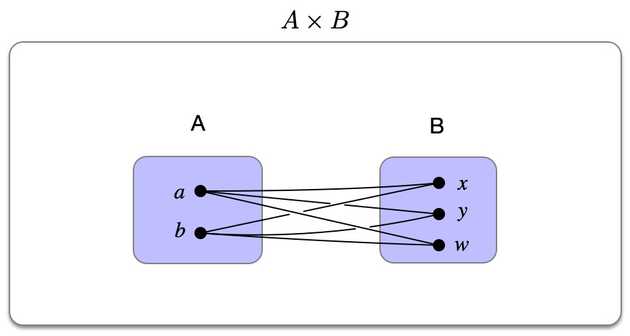
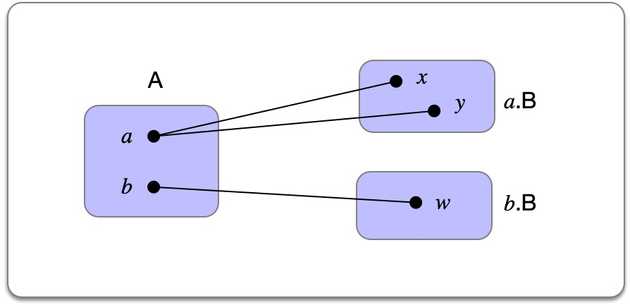
This represents all possible combinations of elements from both sets:

The Dependent pair type $\Sigma (x: A), B(x)$ denotes the type of pairs $(a, b)$ where $a \in A$ and $b \in B(a)$

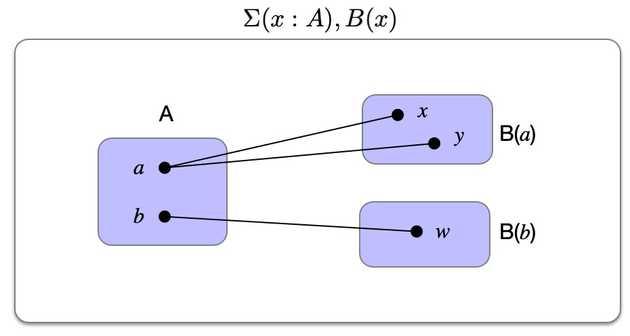
The diagram depicts a situation where $x$ and $y$ are elements of $B(a)$ and $w \in B(b)$. In this case the inhabitants of the dependent pair type $\Sigma (x: A), B(x)$ are the pairs:

4.1 Dependent pairs in Lean

In Lean dependent pairs are defined as the inductive type:

namespace Hidden

universe u v

structure Sigma {A: Type u} (B: A -> Type v) where
  fst: A
  snd: B fst

end Hidden

Dependent pairs can be constructed like so:

Sigma.mk a b

For example, consider a type function like this:

def IntOrString: Bool -> Type
  | true => Int
  | false => String

With it we can create a list of values that are either Int or String, and nothing else:

def elems: List (Sigma IntOrString) := [
    Sigma.mk true (1: Int),
    Sigma.mk true (2: Int),
    Sigma.mk false "a"
  ]

Lean also has notation for dependent pairs: (b: Bool) × IntOrString b (or Σ b, IntOrString b) is the type Sigma IntOrString, and the anonymous constructor ⟨true, (1: Int)⟩ builds Sigma.mk true (1: Int):

def elems': List ((b: Bool) × IntOrString b) := [
    ⟨true, (1: Int)⟩,
    ⟨true, (2: Int)⟩,
    ⟨false, "a"⟩
  ]

Another use case for dependent pairs is to define mathematical structures. For example we could define a Magma type and two instances like so

def Magma := Sigma (fun M => M -> M -> M)

def additiveMagma      : Magma := Sigma.mk Nat (fun a b => a + b)
def multiplicativeMagma: Magma := Sigma.mk Nat (fun a b => a * b)

The type $\Sigma (x: A), B(x)$ can also be interpreted as the proposition "exists $a$ in $A$ such that $B(a)$":

which can be proved by exhibiting at least one element of the set $B(a)$ for some $a: A$.

In Lean, though, ∃ is a separate type, Exists, whose values are proofs: it lives in Prop. The difference matters. From a Sigma we can always get the witness back (fst), but from a proof of ∃ n, n > 0 we can't extract the number n as data:

-- `#check_failure` succeeds only if the expression does NOT type-check:
#check_failure fun (h: ∃ n: Nat, n > 0) => (h.1 : Nat)
-- Invalid projection: Cannot project a value of non-propositional type Nat

Lean treats all proofs of a proposition as equal (proof irrelevance), so a program can't look inside a proof to get the witness.

4.2 Dependent pairs in Scala

Dependent pairs can be encoded directly with path-dependent types.

trait Fn0:
  type B

class Sigma[A <: Fn0](fst: A, snd: fst.B)

Here the family B is modeled as a type member of the first component: snd has type fst.B. So Scala can express a dependent pair only when the type of the second component can be written as a type member of the first value.

In general, every function that uses path-dependent types in its parameters list is an example of Sigma types in action:

def f[A <: Fn0](a: A, b: a.B) = ???

def g[A <: Fn0](s: Sigma[A]) = ???

Next time we'll talk about proofs and tactics. Stay tuned!

Resources

• Type-Driven Development with Idris

• Theorem Proving in Lean 4:

  • Dependent Type Theory
  • Type Classes

• Dependent Function Types: Sections of a Bundle

• Scala 3 reference:

  • Dependent Function Types
  • Match Types
  • Inline