In the previous installment we discussed inductive types and patern matching.
Today we’re going to talk about Dependent Types and Type Classes.
Latest revision: Sep 4, 2022
1. Dependent functions
1.1 Idea
A function between two sets is commonly defined in mathematics as a collection of pairs with the property that elements of appear exactly once.
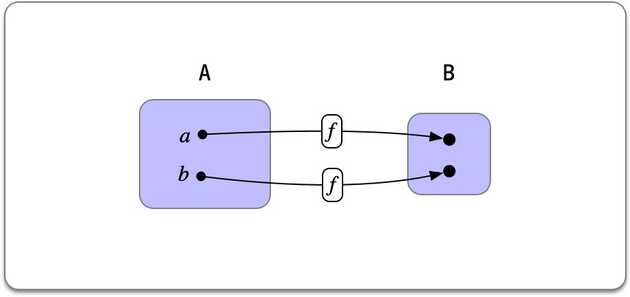
A dependently typed function is a generalization of this concept:
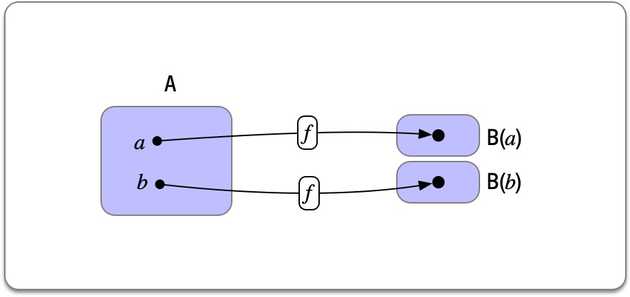
Each element is allowed to be a member of a different set that depends on .
This construction gives rise to a set-level function that assigns a set to each element .
Observe that if this function is constant (i.e. it maps all elements to a single set) then we are back to the regular definition of non-dependent functions.
Example: Vector fields
At every point of a circle , consider a vector on the tangent space at this point:
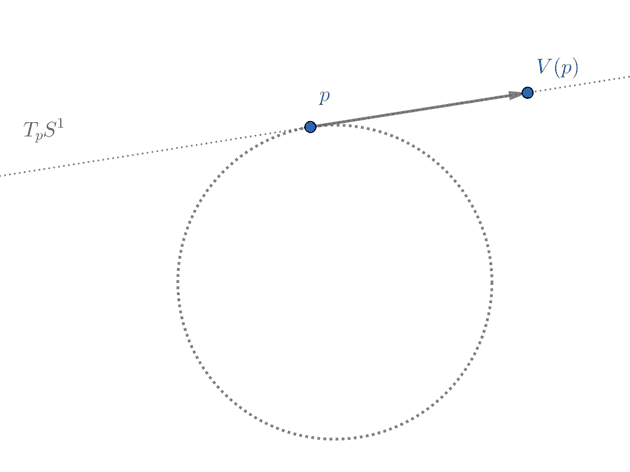
Since each lives in a different tangent space (that depends on ), it makes sense to regard as a dependent function.
Example: operations on tuples
A very common example of dependent types in Scala 3 is obtaining components of tuples at specific positions:
val t: (Int, String, Boolean) = (0, "", false)
assert( t.apply(0) == 0 )
assert( t.apply(1) == "" )
assert( t.apply(2) == false )We can see how apply produces a value of a type that depends on the input index:
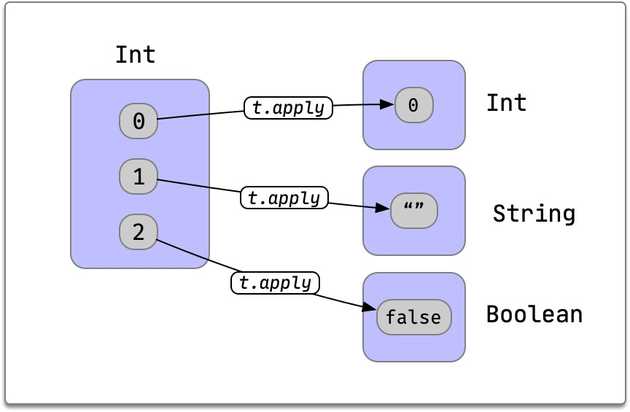
In fact most generic tuple operations use dependent types.
1.2 Dependent functions in Lean
In Lean the type of a regular function from to is written as
f: A -> Bhere the codomain B is the same for every element a of the domain A.
In a dependent function we need a way to indicate exactly how the codomain depends on each element of the domain.
The signature of a dependent function from to is written in Lean like this:
f: (a: A) -> B aExample: variable number of arguments
Consider a function adder that takes:
- A number representing extra arguments
- An initial value
- arguments
and returns the sum of the initial value and extra arguments.
adder 2 acc 4 3 = acc + 4 + 3For example
example: adder 0 5 = (5 : Nat) := rfl
example: adder 1 10 11 = (21: Nat) := rfl
example: adder 2 18 17 12 = (47: Nat) := rfli.e. the first argument is the number of extra arguments after the 2nd argument.
(This example is described in Edwin Brady’s Type-Driven Development with Idris)
We will proceed in two steps:
- Define a type level function that calculates the return type: a function with parameters:
def Adder: Nat -> Type
| 0 => Nat
| k + 1 => Nat -> Adder k
example: Adder 0 = Nat := rfl
example: Adder 1 = (Nat -> Nat) := rfl
example: Adder 2 = (Nat -> Nat -> Nat) := rfl- Define a regular function, whose signature is computed by
Adderbased on the 1st argument:
def adder: (n: Nat) -> (acc: Nat) -> (Adder n)
| 0, acc => acc
| k + 1, acc => fun n => adder k (n + acc)
-- some examples of types:
-- adder 0 : Nat -> Nat
-- adder 1 : Nat -> Nat -> Nat
-- adder 2 : Nat -> Nat -> Nat -> Nat
example: (adder 0) 5 = (5 : Nat) := rfl
example: (adder 1) 10 11 = (21: Nat) := rfl
example: (adder 2) 18 17 12 = (47: Nat) := rflSo adder n produces a function whose type depends on n:
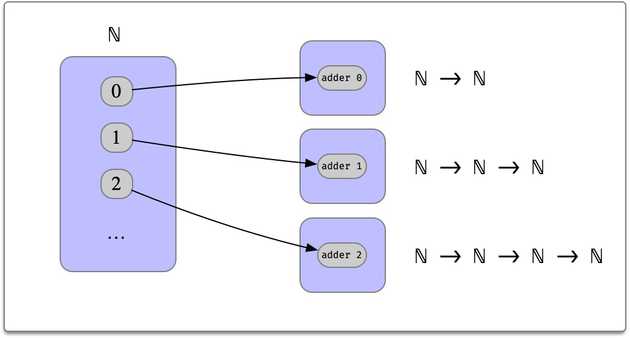
1.3 Dependent Functions in Scala 3
Match types
Scala 3 supports a similar form of dependent typing using match types.
We follow the same steps as in Lean:
- Define a type level function that calculates the return type:
import compiletime.ops.int.S
type Adder[N <: Int] = N match
case 0 => Int
case S[k] => (Int => Adder[k & Singleton])
summon[ Adder[0] =:= Int ]
summon[ Adder[1] =:= (Int => Int) ]
summon[ Adder[2] =:= (Int => Int => Int)]- Define a function, whose signature is computed by
Adderbased on the 1st argument:
inline def adder[N <: Int & Singleton](n: N)(acc: Int): Adder[N] =
inline n match
case _: 0 => acc
case _: S[k] => n => adder(constValue[k & Singleton])(n + acc)
assert( adder(0)(5) == 5 )
assert( adder(1)(10)(11) == 21 )
assert( adder(2)(18)(17)(12) == 47 )Here we can see how the fact that types are not first class in Scala introduces some complexities:
Singletonis needed so thatadder(0)is inferred asadder[0](0)and notadder[Int](0).- After pattern matching on the type
_: S[k]we obtain the typekof the predecessorn - 1. - In order to continue the process we need to obtain the value associated with the singleton type
k. For this we useconstValue. - But
constValueonly works for values known at compile time, so we have to use inline match and also inline the whole function.
2. Type Classes
Type Classes can be used as a mechanism to represent dependent types.
2.1 Type Classes in Lean
Lean has support for type classes by using the keywords class / instance.
Let’s implement the adder function using implicit type class resolution this time:
class Bundle (n: Nat) where
Adder: Type
adder: Nat -> AdderThis declaration defines a few things:
| A type | Bundle |
: |
Nat → Type 1 |
| A namespace | Bundle |
||
| A constructor function | Bundle.mk |
: |
{n : Nat} → (Adder : Type) → (Nat → Adder) → Bundle n |
| A field | Bundle.Adder |
: |
(n : Nat) → [self : Bundle n] → Type |
| A field | Bundle.adder |
: |
{n : Nat} → [self : Bundle n] → Nat → Bundle.Adder n |
Note how both Bundle.Adder and Bundle.adder acquired two extra parameters:
- The class argument
(n: Nat) - An implicit instance
[self : Bundle n](indicated by the square brackets)
In order to use the function Bundle.adder the number n needs to be known, either by inference or explicitly providing it like so:
#eval Bundle.adder (n := 0) 5
-- 5
#eval Bundle.adder (n := 1) 10 11
-- 21Alternatively we can create a helper function where n is required explicitly
def adder (n acc: Nat) [c: Bundle n]: Bundle.Adder n :=
@Bundle.adder n c acc
#eval adder 0 5
-- 5
#eval adder 1 10 11
-- 21We need two Bundle instances again, corresponding to the base case and the inductive step:
instance : Bundle 0 where
Adder := Nat
adder := id
instance (k: Nat) [predecessor: Bundle k] : Bundle (k + 1) where
Adder := Nat -> predecessor.Adder
adder := fun acc n => Bundle.adder (n + acc)Notes:
idis the identity functionadder k (n + acc)is using the implicit instance in scope (predecessor), so we don’t need to pass it manually.
Sanity check:
example: (adder 0) 5 = (5 : Nat) := rfl
example: (adder 1) 10 11 = (21: Nat) := rfl
example: (adder 2) 18 17 12 = (47: Nat) := rfl2.2 Type Classes in Scala
The same type class in Scala:
trait Bundle[N <: Int]:
type Adder
def adder: Int => AdderDue to a idiosyncrasy of Scala we need to create a helper type function BundleWithAdder to manually propagate type information (this is the Aux pattern common in shapeless).
type BundleWithAdder[N <: Int, A] =
Bundle[N] { type Adder = A }
// base case: Bundle[0]
given BundleWithAdder[0, Int] =
new Bundle[0]:
type Adder = Int
def adder = identity
// inductive step: Bundle[K] implies Bundle[S[K]]
given [K <: Int](using predecessor: Bundle[K]):
BundleWithAdder[S[K], Int => predecessor.Adder] =
new Bundle[S[K]]:
type Adder = Int => predecessor.Adder
def adder = acc => n => predecessor.adder(n + acc)Sanity check:
val bundle0 = summon[Bundle[0]]
val bundle1 = summon[Bundle[1]]
val bundle2 = summon[Bundle[2]]
summon[ bundle0.Adder =:= Int ]
summon[ bundle1.Adder =:= (Int => Int) ]
summon[ bundle2.Adder =:= (Int => Int => Int) ]Taking the singleton type n.type of the term n will kickstart the process:
def adder(n: Int)(acc: Int)(using bundle: Bundle[n.type]) =
bundle.adder(acc)
assert( adder(0)(5) == 5 )
assert( adder(1)(10)(11) == 21 )
assert( adder(2)(18)(17)(12) == 47 )3. Propositions depending on values.
Propositions can be used as goals unto themselves (example 3.1) or as a way to create specifications (example 3.2).
3.1 Properties of natural numbers
Consider the statement:
For all natural numbers,
The expression is a proposition that depends on , and so the statement can be modeled as a dependent function from natural numbers to a family of propositions:
example (n : Nat) : n + 0 = n :=
rfl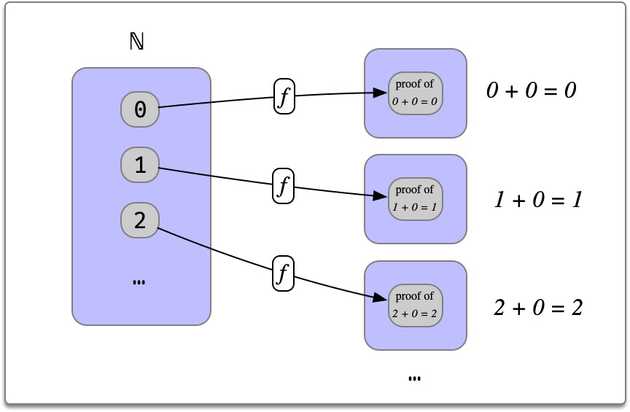
3.2 Algebraic structures
Here’s how one could define a monoid in Lean
class Monoid (M) where
mul : M -> M -> M
one : M
mul_assoc : ∀ (a b c : M), mul (mul a b) c = mul a (mul b c)
one_mul : ∀ (a : M), mul one a = a
mul_one : ∀ (a : M), mul a one = aIn this kind of situations we rely heavily on dependent types to encode all the laws associated with the structure at hand. In this example each law is a dependent function from M to propositions.
Here’s a monoid instance for addition of natural numbers:
instance : Monoid Nat where
mul := (· + ·)
one := 0
mul_assoc := Nat.add_assoc
one_mul := Nat.zero_add
mul_one := Nat.add_zeroLuckily in this case the basic properties have already been proved in the std library, so we can just delegate to them.
- The expression
(· + ·)is the short form of the anonymous functionfun a b => a + b, similar to Scala’s_ + _.
4. Dependent pairs
There is another important example of dependent types called Dependent pairs or -types (or even dependent products).
Consider the regular cartesian product of two sets , :
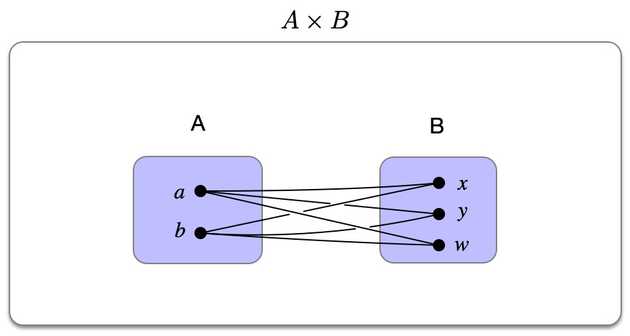
This represents all possible combinations of elements from both sets:
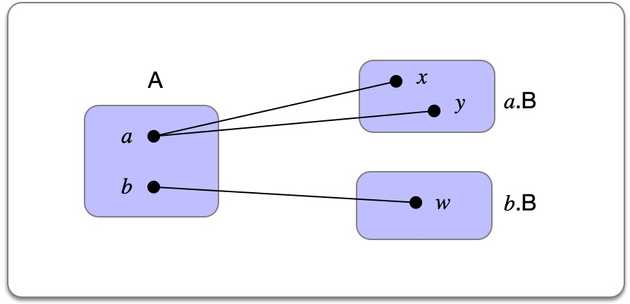
The Dependent pair type denotes the type of pairs where and
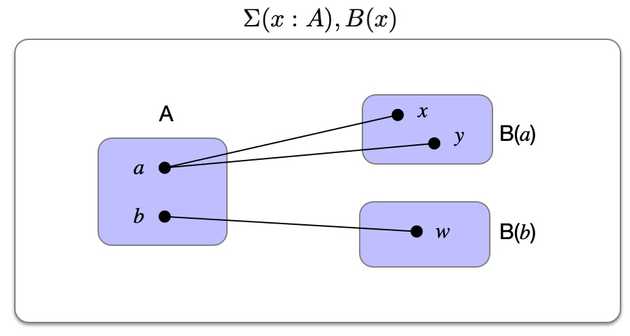
The diagram depicts a situation where and are elements of and . In this case the inhabitants of the dependent product are the pairs:
4.1 Dependent pairs in Lean
In Lean dependent pairs are defined as the inductive type:
universes u v
structure Sigma {A: Type u} (B: A -> Type v) where
Fst: A
snd: B FstDependent pairs can be constructed like so:
Sigma.mk a bFor example, consider a type function like this:
def IntOrString: Bool -> Type
| true => Int
| false => StringWith it we can create a list of values that are either Int or String, and nothing else:
def elems: List (Sigma IntOrString) := [
Sigma.mk true (1: Int),
Sigma.mk true (2: Int),
Sigma.mk false "a"
]Another use case for dependent pairs is to define mathematical structures. For example we could define a Magma type and two instances like so
def Magma := Sigma (fun M => M -> M -> M)
def additiveMagma: Magma := Sigma.mk Nat (fun a b => a + b)
def multiplMagma : Magma := Sigma.mk Nat (fun a b => a * b)The type can also be interpreted as the proposition “exists in such that “:
which can be proved by exhibiting at least one element of the set for some .
(Although Lean has a type Exists just for this scenario)
4.2 Dependent products in Scala
Dependent products can be encoded directly with path-dependent types.
trait Fn0:
type B
class Sigma[A <: Fn0](fst: A, snd: fst.B)In general, every function that uses path-dependent types in its parameters list is an example of Sigma types in action:
def f[A <: Fn0](a: A, b: a.B) = ???
def g[A <: Fn0](s: Sigma[A]) = ???Next time we’ll talk about proofs and tactics. Stayed tunned!
Resources
-
Theorem Proving in Lean:
-
Scala 3 manual: