A: Type vs A <: Any

Types in Lean are first-class objects, meaning that they can be treated as regular values: they have a type, they can be stored, passed around, returned from functions. So A: Type means that A is a type.

Since every expression has a type, it is natural to ask: what is the type of Type? Turns out there is a type called Type 1 that has Type as an inhabitant.

Type : Type 1

and a type Type 2 that has Type 1 as an inhabitant.

Type 1 : Type 2

and so on.

In fact, Type is just an alias for Type 0 and we have an infinite tower of types

...
Type 2 : Type 3
Type 1 : Type 2
Type 0 : Type 1

It’s types all the way up!

Graphically:

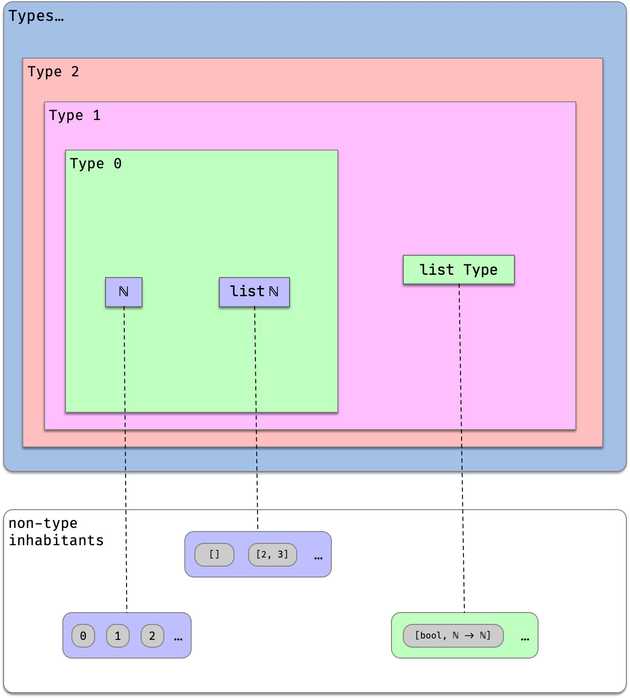
In this diagram the boxes at the top are types, and their inhabitants (also types) are displayed inside. The inhabitants that are not types (such as regular numbers) are displayed at the bottom, connected by broken lines.

Each concrete number i above is called a universe level.

Note that list Nat has type Type 0, whereas list Type has type Type 1.

If we want to declare type variables of any universe we can use the syntax {A: Type _} like so:

Lean 4:

def length' {A: Type _}: List A -> Nat
  | []     =>  0
  | _ :: t =>  1 + length' t 

In Lean, propositions are types that sit at the bottom of the universe hierarchy:

...
Type 2 : Type 3
Type 1 : Type 2
Type 0 : Type 1
Nat    : Type 0 
Prop   : Type 0
2 = 3  : Prop
2 = 2  : Prop
rfl 2  : 2 = 2
...

Graphically:

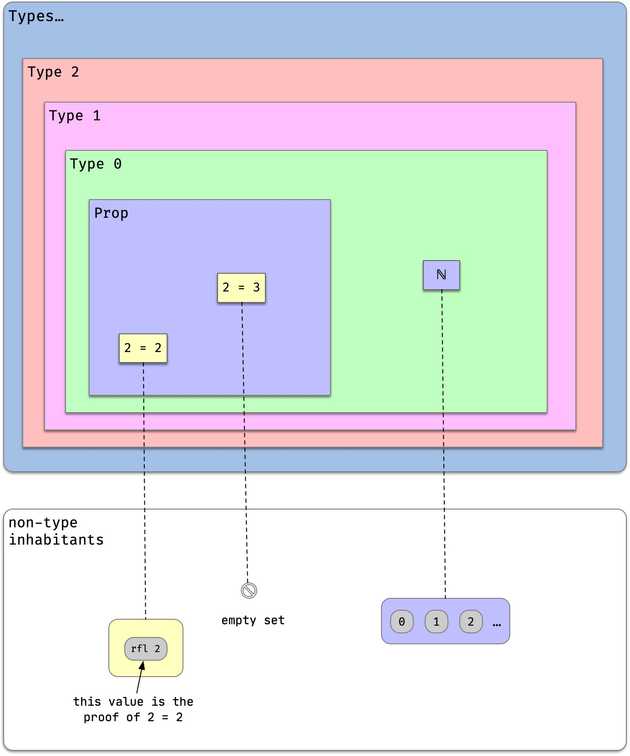
You can see that Type 0 has Prop as an inhabitant (alongside with Nat, and others not shown). Prop’s own inhabitants (such as 2 = 2, 2 = 3) are types as well.